• The basic maths class 10 formulas are almost the same for all the boards. The list

  of maths formulas are: 

  1. Pair of Linear Equation in Two Variables Formulas
  2. Algebra andQuadratic Equation Formulas
  3. Arithmetic Progression Formulas
  4. Trigonometry Formulas
  5. Circle Formulas
  6. Surface Area andVolume Formulas
  7. Statistics Formulas

                  Linear Equations

• One Variable ax+b=0 a≠0 and a&b are real numbers
• Two variable ax+by+c = 0 a≠0 & b≠0 and a,b & c are real numbers
• Three Variable ax+by+cz+d=0 a≠0 , b≠0, c≠0 and a,b,c,d are real numbers
• Pair of Linear Equations in two variables:

a1 x+b1+c1=0

a2 x+b2+c2=0

• Where

a1, b , c1 , a2 , b2 , and c2 are all real numbers .

▪It should be noted that linear equations in two variables  can also be represented in graphical form.

           Algebra or Elgebraic Equation 

1. The standard form of Quadratic Equations: ax +bx+c=0 where a ≠ 0 And x = [-b ± √(b – 4ac)]/2ac

2. Algebraic formulas:

   • (a+b)2=a2+2ab+b2
   • (a-b)2 = a2+ b2– 2ab
   • (a+b) (a-b) = a2 – b2
   • (x + a)(x + b) = x2+ (a + b)x + ab
   • (x + a)(x – b) = x2+ (a – b)x – ab
   • (x – a)(x + b) = x2+ (b – a)x – ab
   • (x – a)(x – b) = x2– (a + b)x + ab
   • (a + b)3 = a3+ b3+ 3ab(a + b)
   • (a – b)3= a3– b3– 3ab(a – b)
   • (x + y + z)2 = x2+ y2+ z2+ 2xy + 2yz + 2xz
   • (x + y – z)2 = x2+ y2+ z2+ 2xy – 2yz – 2xz
   • (x – y + z)2 = x2 + y2– 2xy – 2yz + 2xz
   • (x – y – z)2= x2 + y2 + z2 – 2xy + 2yz – 2xz
   • x3 + y3 + z3 – 3xyz = (x + y + z)(x2 + y2 + z2 – xy – yz -xz)
   • x2+ y2=½ [(x + y)2 + (x – y)2 ]
   • (x + a) (x + b) (x + c) = x3 + (a + b +c)x2 + (ab + bc + ca)x + abc
   • x3 + y3 = (x + y) (x2 – xy + y2 )
   • x3 – y3= (x – y) (x2 + xy + y2 )
   • 2+ y + z2-xy – yz – zx = ½ [(x-y)2 + (y-z)2 + (z-x)2 ].
   • 
     

Arithmetic Progression(AP) Formulas

1. If a1, a2, a3 ,a4, a5 , a6 , are the terms of AP and d is the common difference

between each term, then we can write the  sequence as; a, a+d, a+2d, a+3d, a+4d,

a+5d,….,nth term… where a is the first term.

Now, n term for arithmeticprogression is given as;

• nth term in Arithmetic Progression = a + (n-1) d
• Sum of n term in Arithmetic Progression;

       S = n/2 [a + (n-1) d]

   Trigonometry Formulas For Class 10

• Trigonometry maths formulas for Class 10 covers three major functions Sine,

   Cosine and Tangent for a right-angle triangle. Also, in trigonometry the functions sec, cosec and cot formulas can be derived with the help of sin, cos and tan formulas.

• Let a right-angled triangle ABC is right-angled at point B and have
• Sinθ=Sideoppositetoangleθ/Hypotenuse=Perpendicular/Hypotenuse = P/H
• Cos θ = adjacent/hypotenuse=  B/H
• Tan θ = Opposite / Adjacent= P/B
• Sec θ = Hypotenuse / Base = 1/cosθ
  
• Cot θ =  Adjacent / Opposite  = 1/tan θ.
• Cosec θ = Hypotenuse/ Perpendicular= 1/ sin ϴ
• Tan θ = sin θ / cos θ
• cot θ = cos θ / sin θ

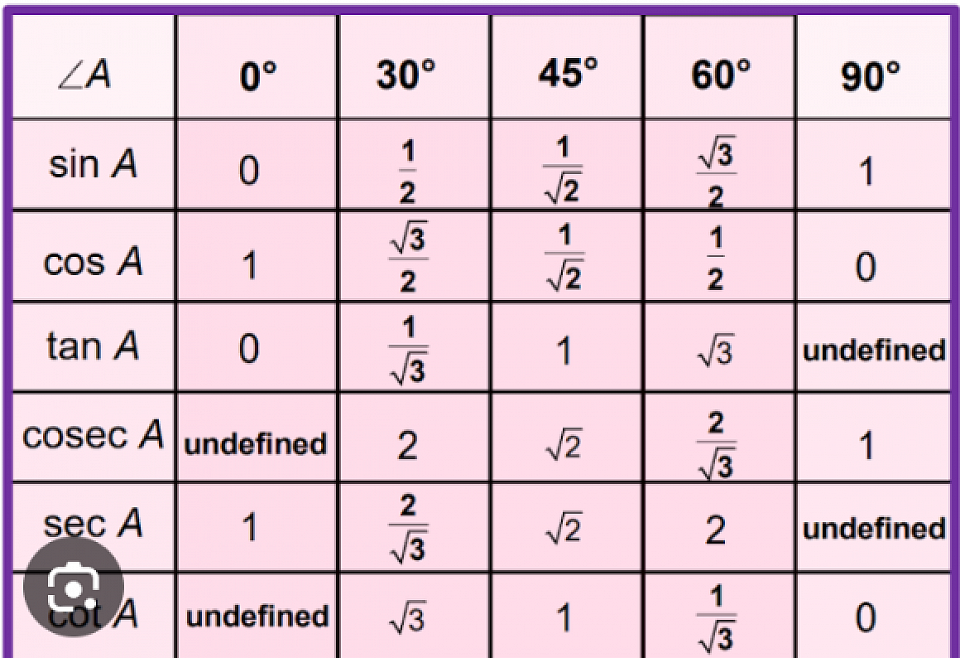
1. Trigonometry Table

Circles Formulas For Class 10

• Circumference of the circle = 2 π r
• Area of the circle = π r2
• Area of the sector of angle θ = (θ/360) × π r2
• Length of an arc of a sector of angle θ = (θ/360) × 2 π r

(r = radius of the circle)

1. Diameter of sphere = d = 2r
2. Circumference of sphere = 2 π r
3. Surface area of sphere=4 π r2
4. Volume of sphere = 4/3 π r3

1. Circumference of Cylinder =2 πrh
2. Curved surface area of Cylinder =2 πr2
3. Total surface area of Cylinder  = Circumference of Cylinder + Curved surface area ofCylinder = 2 πrh + 2 πr2 =2πr(h+r)
4. Volume of Cylinder = π r2 h
   

• Slant height of cone l = √(r2 + h2 )
• Curved surface area of cone = πrl
• Total surface area of cone = πr (l + r)

• Volume of cone = ⅓ π r2 h

• Perimeter of cuboid = 4(l + b +h)
• Length of the longest diagonal of a cuboid = √(l2+ b2+ h2 )
• Total surface area of cuboid = 2(l×b + b×h + l×h)
• Volume of Cuboid = l × b × h

Here, l = length, b = breadth and h = height In case of Cube, put l = b = h = a, as cube all its sides of equal length, to find the surface area and volumes.

Statistics Formulas for Class 10

In class 10, the chapter statistics mostly deals with finding the mean median and standard deviation of grouped data.

• (|)The mean of grouped data: calculate the mean (or average) of a set of numbers, you add all the numbers together and then divide the sum by the total number of values in the set. 

• The mean of the grouped data can be found by 3 methods.
• 1. Direct Method:

        Mean (x̄) = (Σ(f * x)) / Σ(f) 

• x̄ is the mean
• f is the frequency of each class
• x is the class midpoint
• Σ(f * x) is the sum of the product of frequency and class midpoint
• Σ(f) is the sum of all frequencies 

• value i = 1 to n And f is the number of observations from value i = 1 to n
• 2. Assumed mean method : 

        Mean (x̄) = a + ( Σfidi / Σfi ) 

• 'a' is the assumed mean.
•  'di' is the deviation of each class mark (xi) from the assumed mean (a) (di = xi - a).
•  'fi' is the frequency of each class interval. 
• Σfidi is the sum of the product of frequencies and deviations. 
• Σfi is the sum of the frequencies. 
  
• 3. Step deviation method :

        Mean (x̄) = a + (h * Σfui / Σfi) 

• 'a' is the assumed mean.
•  'h' is the class size (width of the class interval). 
• 'ui' is the step deviation, calculated as ui = (di / h) or ui = (xi - a) / h. 
• 'fi' is the frequency of each class interval. 
• Σfui is the sum of the product of frequencies and step deviations. 
• Σfi is the sum of the frequencies. 
  
• (II) The mode of grouped data:The mode is a measure of central tendency, representing the value that occurs most often in a dataset. 

         Mode  = L + [(f1 - f0) / (2f1 - f0 - f2)] * h

• L: Lower limit of the modal class (the class with the highest frequency).
• h: Size of the class interval (the difference between the upper and lower limits of the class).
• f1: Frequency of the modal class.
• f0: Frequency of the class preceding the modal class.
• f2: Frequency of the class succeeding the modal class.
  
• (III) The median for a grouped data:To calculate the median, first arrange the data in ascending order. If the number of data points is odd, the median is the middle value; if even, it's the average of the two middle values.
• Median  = [ (n/2)th value + (n/2 + 1)th value ] / 2